Material
Introduction
Chirplet Transforms. The chirplet transform is an inner product of an input signal with a family of analysis primitives called chirplets. The chirplet transform of \(f\in L^2(\mathbb{R})\) given a window function \(g\) at \((t, \xi, \lambda)\) is defined as
\[T_f^{(g)}(t,\xi,\lambda)= \int_{\mathbb{R}}f(x)g(x-t)e^{-2\pi i \xi (x-t)-\pi i\lambda(x-t)^2}dx\]where \(t\in\mathbb{R}\) indicates time, \(\xi \in\mathbb{R}\) indicates frequency, and \(\lambda\in\mathbb{R}\) indicates the chirp rate. We can see that the inner product basis \(e^{i\pi(2x\xi+x^2\lambda)}\) is different from \(e^{i\pi 2x\xi}\).
We can intuitively see that if we set \(f(x) = e^{2\pi i \xi_0 + \pi i \lambda_0 x^2}\), then \(T_f^{(g)}(t,\xi,\lambda)\) is sufficient closed to \(\xi_0+\lambda_0 t\). Please see Mann et al. (1995) for more detail.
Synchrosqueezed Transforms. The synchrosqueezed transform is a time-frequency analysis method that is useful for analyzing multicomponent signals with oscillating modes because this method reassigns the signal energy in frequency to lead the time-frequency plan to be clearer.
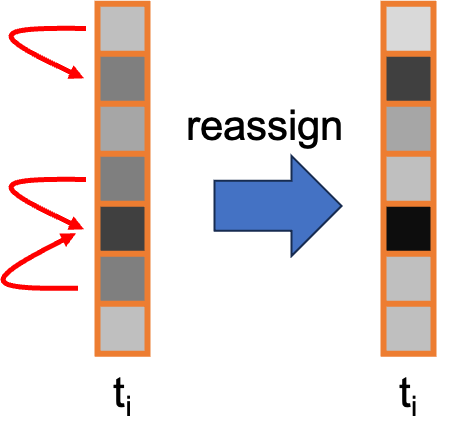
Please see Daubechies et al. (2011) for more detail.
Synchrosqueezed Chirplet Transforms. By put above two things together, for each specific time, this method will reassigns the signal energy in frequency-chirp plan rather than frequency axis. Please see Chen & Wu (2023) for more detail.
Higher Order Synchrosqueezed Chirplet Transforms
TBA in Feb.
Results
\(\begin{aligned} & x_1=\exp \left(j 2 \pi\left(4 t^2\right)\right) \rightarrow f_1=8 t \\ & x_2=\exp \left(j 2 \pi\left(-\pi t^2+(24+6 \pi) t\right)\right) \rightarrow f_2=-2 \pi t+(24+6 \pi) \\ & x=x_1+x_2 \end{aligned}\)
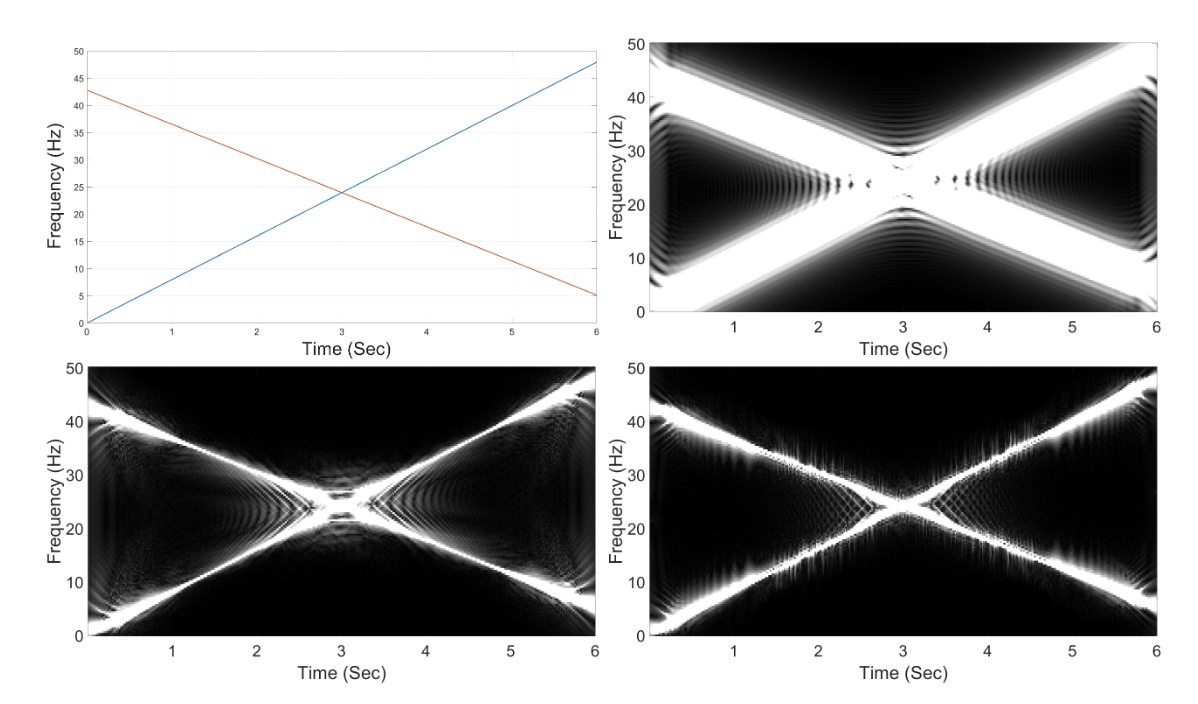
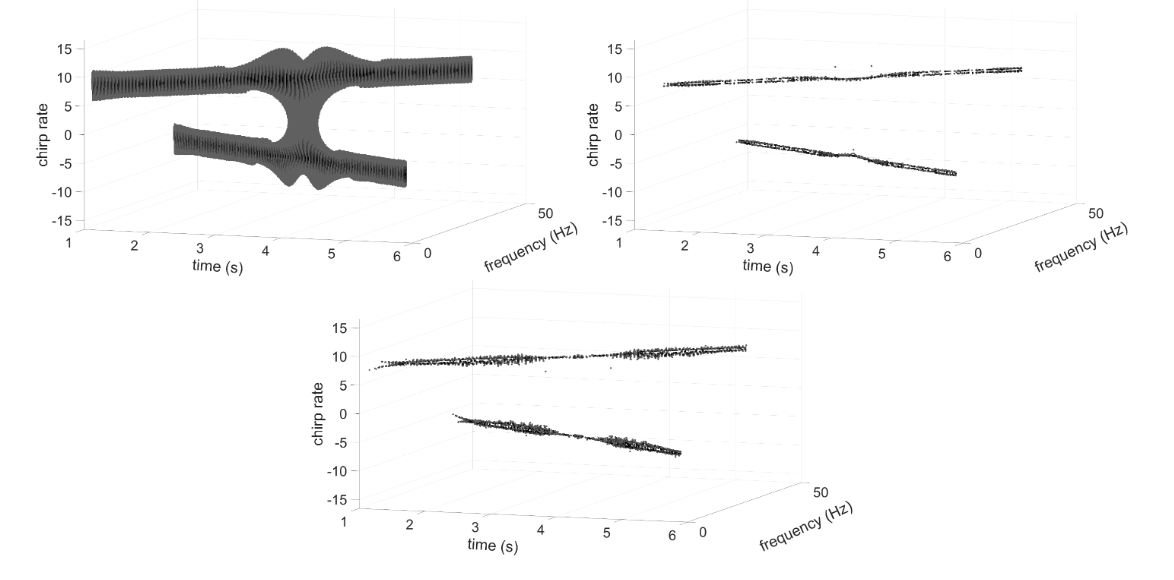
References
- Z. Chen & H.-T. Wu, Disentangling modes with crossover instantaneous frequencies by synchrosqueezed chirplet transforms, from theory to application, (2023).
- I. Daubechies, J. Lu & H.-T. Wu, Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool, (2011).
- S. Mann & S. Haykin, The chirplet transform: physical considerations, (1995).
