Introduction
Vector diffusion maps (VDM) is a tools for organizing complex data sets, embedding them in a low dimensional space, and interpolating and regressing vector fields over the data. VDM is a mathematical and algorithmic generalization of diffusion maps, which is a non-linear dimensionality reduction method based on eigenvectors and eigenvalues of discrete graph Laplacians. The following figure shows the relation between DM and VDM.
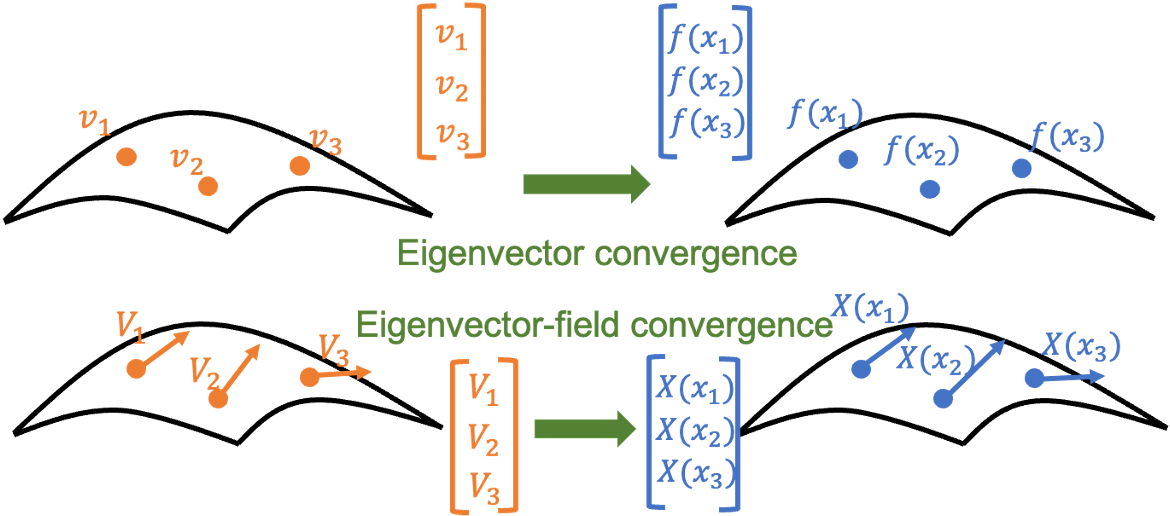
In recently paper, pointwise convergence of the graph connection Laplacian to the connection Laplacian of the tangent bundle is proved in Singer and Wu (2011). Furthermore, the eigenvectors and eigenvalues of the graph Laplacian converge to the eigenfunctions and eigenvalues of the Laplace-Beltrami operator in \(L^2\) sense is proved in Singer & Wu (2015). Thus, this project is focus on proving the spectral convergence of VDM in \(L^\infty\) sense.
| pointwise conv | spectral conv in \(L^2\) | spectral conv in \(L^\infty\) | |
|---|---|---|---|
| DM | Coifman & Lafon (2006) and Singer (2006) | Belkin & Niyogi (2006) | Dunson, Wu & Wu (2019) |
| VDM | Singer & Wu (2011) | Singer & Wu (2015) | this project |
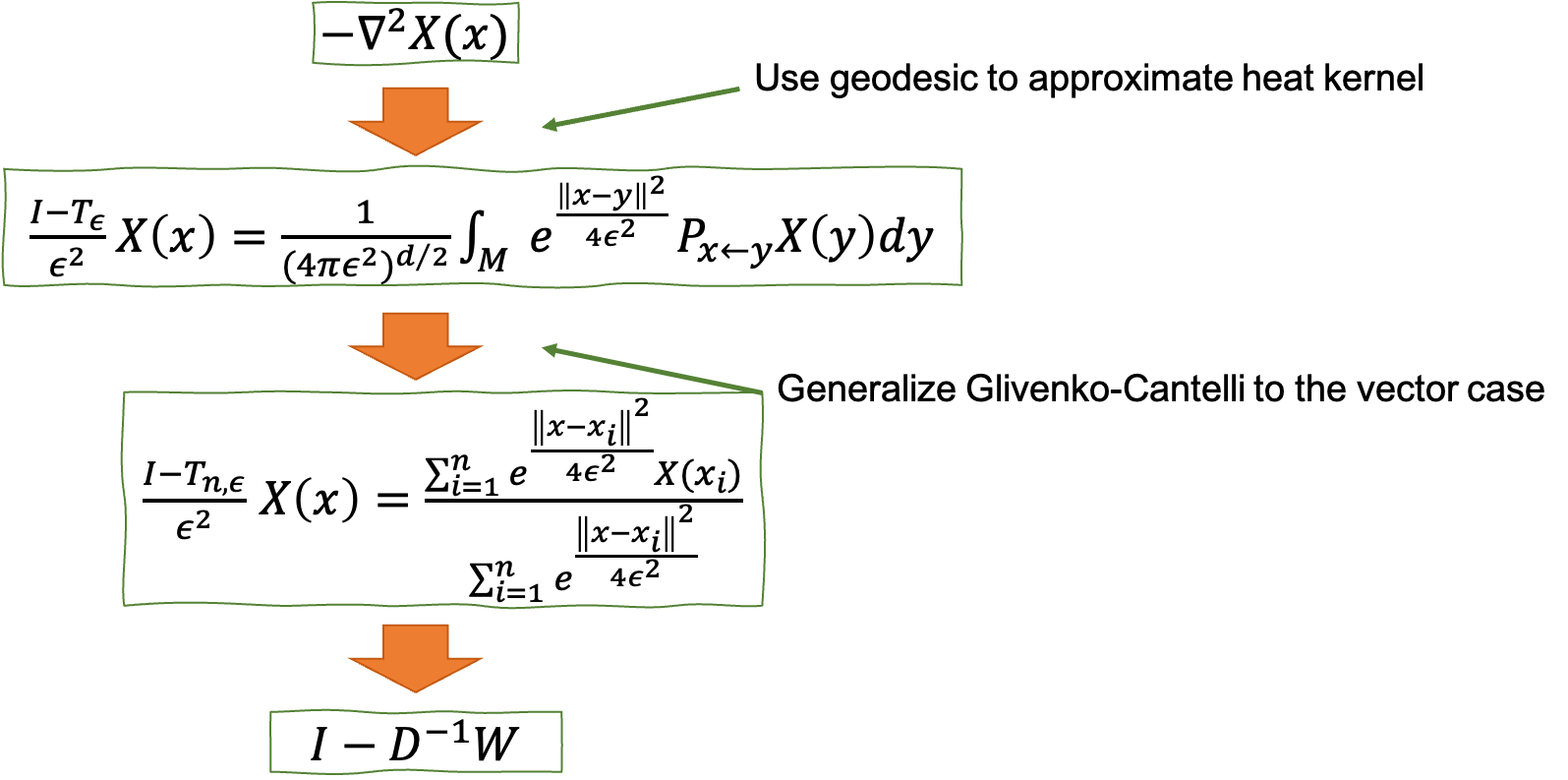
Main Idea of Proof
Due to the results not being published yet, I cannot disclose too much information at this point. Hence, we sketched the proof here.
References
- M. Belkin and P. Niyogi, Convergence of laplacian eigenmaps, (2006).
- R. R. Coifman and S. Lafon, Diffusion maps, (2006).
- D. B. Dunson, H.-T. Wu, and N. Wu, Spectral convergence of graph laplacian and heat kernel reconstruction in l infinity norm from random samples, (2019).
- A. Singer, From graph to manifold laplacian: The convergence rate, (2006).
- A. Singer and H.-T. Wu, Spectral convergence of the connection laplacian from random samples, (2015).
- A. Singer and H.-T. Wu, Vector diffusion maps and the connection laplacian, (2011).
