Introduction
Choptuik presented a numerical study of spherically symmetric collapse of Einstein scalar field equations. Given a initial scalar field \(\psi(r)\) and zero initial velocity of such scalar field \(\psi^\prime (r)=0\) in space (radius coordinates) \(r\), we focus the scalar fields evolve in the future, especially near origin.

The following video is shown how the scalar fields transport. This is weak solution because the incoming scalar field can pass through origin, which cannot collapse the spacetime.
Hence, we want to know how large of the amplitude \(A\) of the initial scalar fields \(\psi_A(r)\) will collapse the spacetime, i.e. incoming scalar fields “freeze” at origin. In this thesis, the initial scalar field is considered as \(\psi_A(r)=Ar^2e^{-(r-5)^2}\). The amplitude of above video is \(A=0.0001\).
Goals
The spherically symmetric metric can be wriiten as \(g=\alpha(r,t)^2dt^2+a^2(r,t)dr^2+r^2d\Omega^2\). Then, we use Einstein scalar fields \(G_{\mu\nu}=8\pi T_{\mu\nu}\)to solve functions \(a(r,t)\) and \(\alpha(r,t)\).
It seems that the numerical simulation of such evolution system is quite trivial. However, we have to face the following problem when we apply finite difference method.
- Stability and Converge Problem: The evolution system is highly nonlinear system so the high order numerical method might not converge.
- Outer Boundary Problem: The computational domain is a finite region but the real space is infinite region. How to impose artificial boundary represents infinite space, which cannot violate the constraint equations.
- Inner Boundary Condition: We will face the operator \(\frac{1}{r^2}\partial_r\). Hence, the origin is become singular and the error will turn large near origin.
Hence, the aim of my thesis is contained the following topic,
- Confirms the simulative results of Choptuik and summarizes useful numerical techniques.
- Summarize the analysis of numerical schemes for solving spherical symmetric Einstein’s equations.
- A survey of the well-posed boundary condition will be introduced.
Results
Weak Solutions
The amplitude \(A=0.0001\) is chosen. As we can see, the evolution of scalar field behaves as we would expect for evolution in flat spacetime.
Besides, Figure shows the value of the lapse function \(\alpha\) at origin drop to near 0.6 when the incoming pulse reaches the origin. However, since the scaler field is not large enough to collapse to a black hole, the value of \(\alpha\) at origin finally returns to 1.
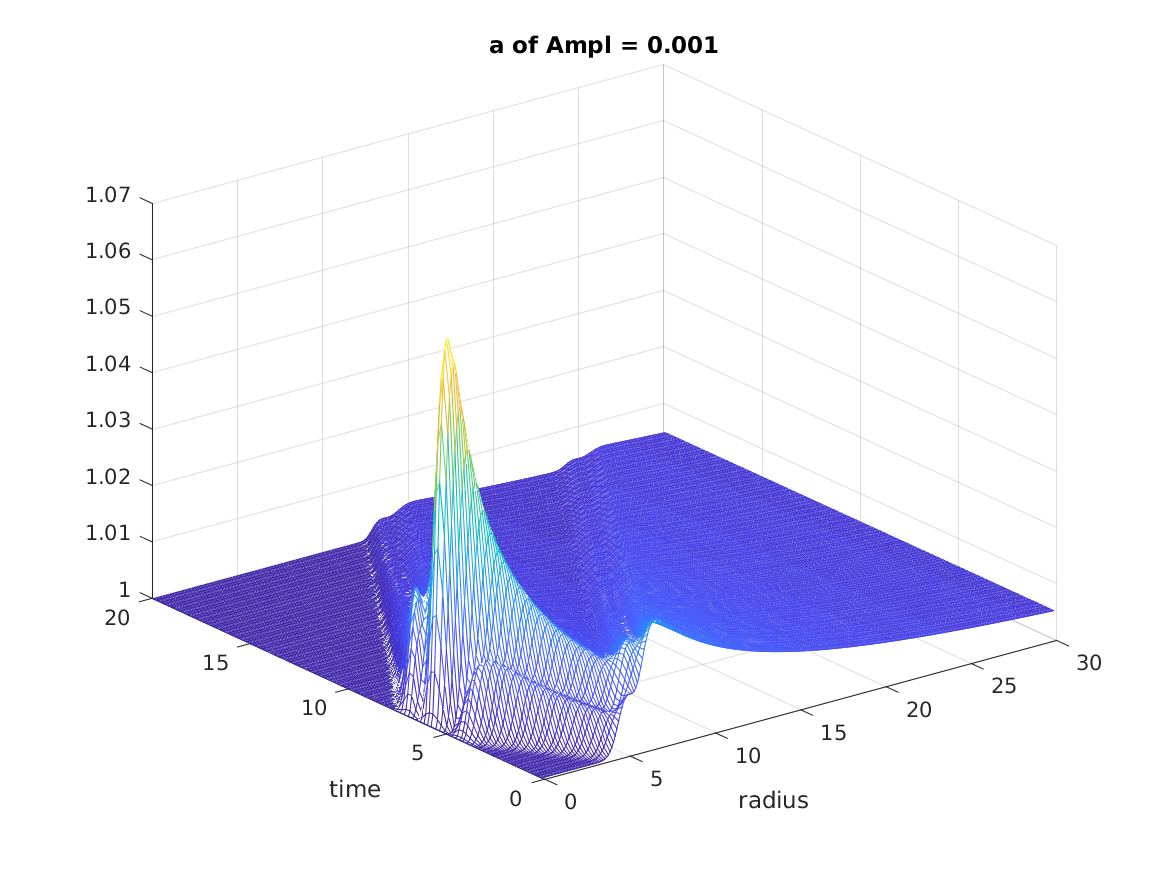
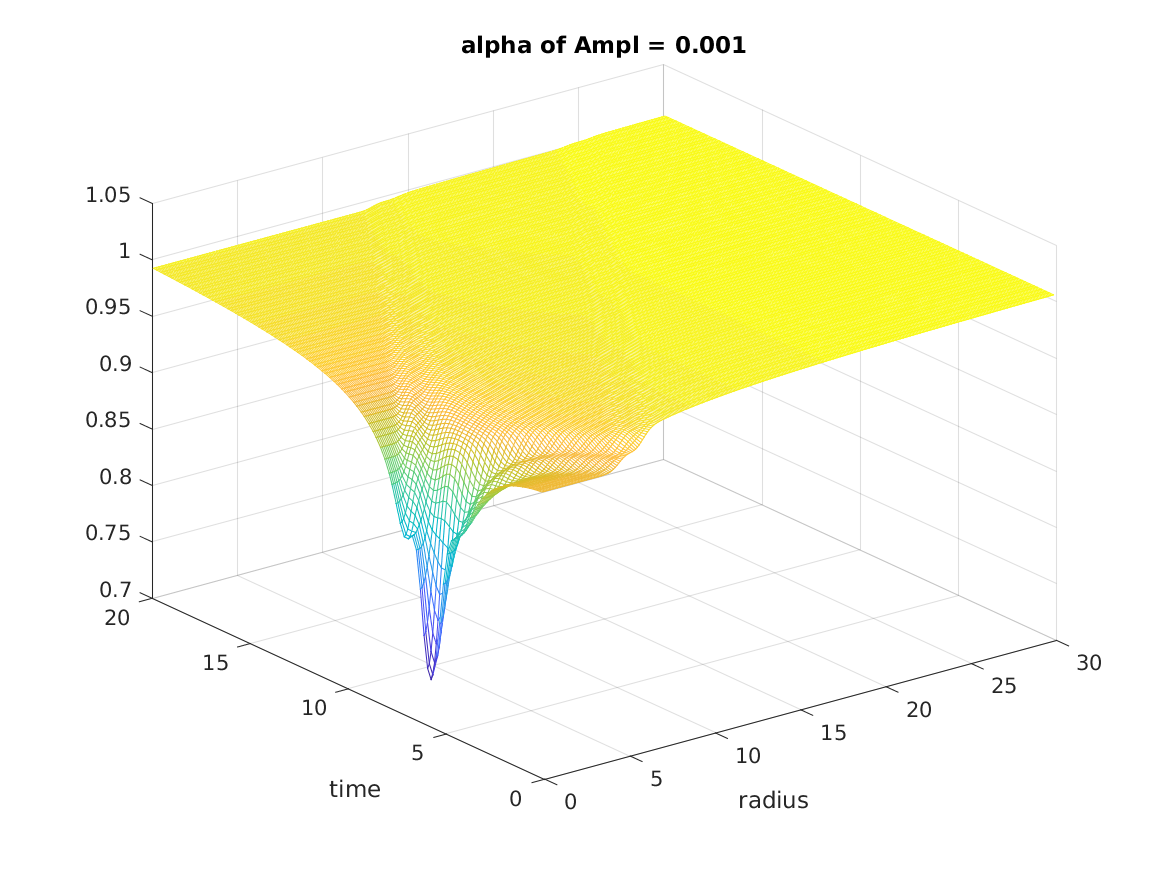
Strong Solutions
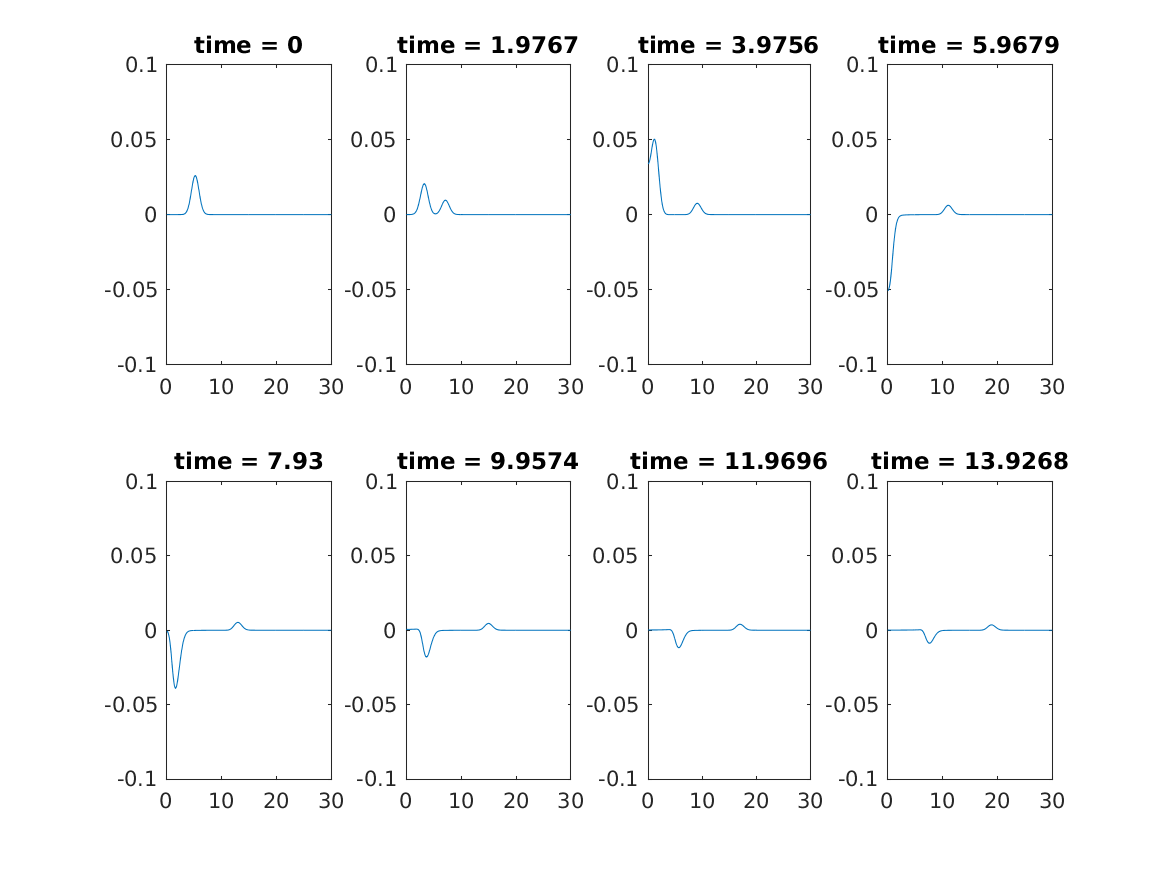
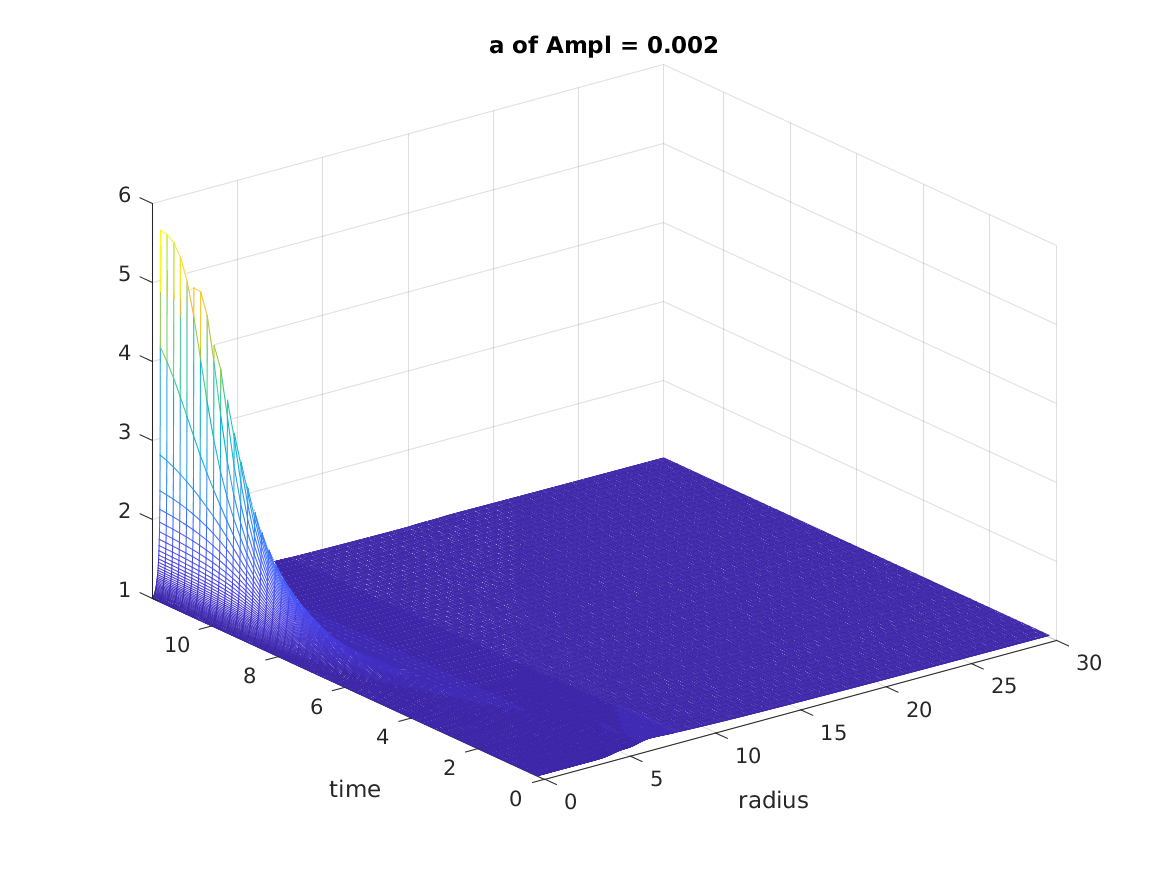
The strong scalar field with amplitude \(A = 0.002\) is implemented below. The scalar field is presented in as following figure. The significant phenomenon can be observed that the scalar field is “freezing” near origin.
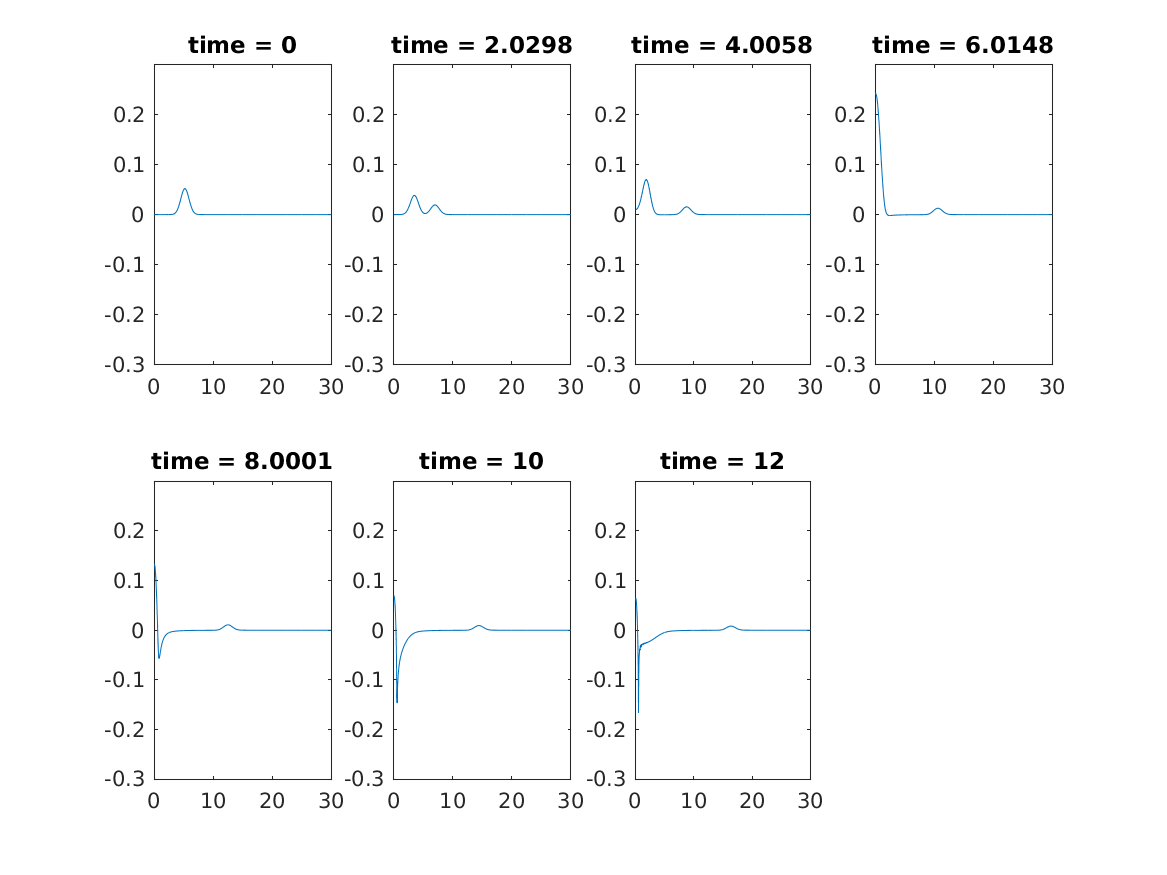
The lapse function \(\alpha\) at origin approaches to 0 as time evolves. Since the lapse is near zero in the central regions, the evolution stops near origin, freezing the scalar field.
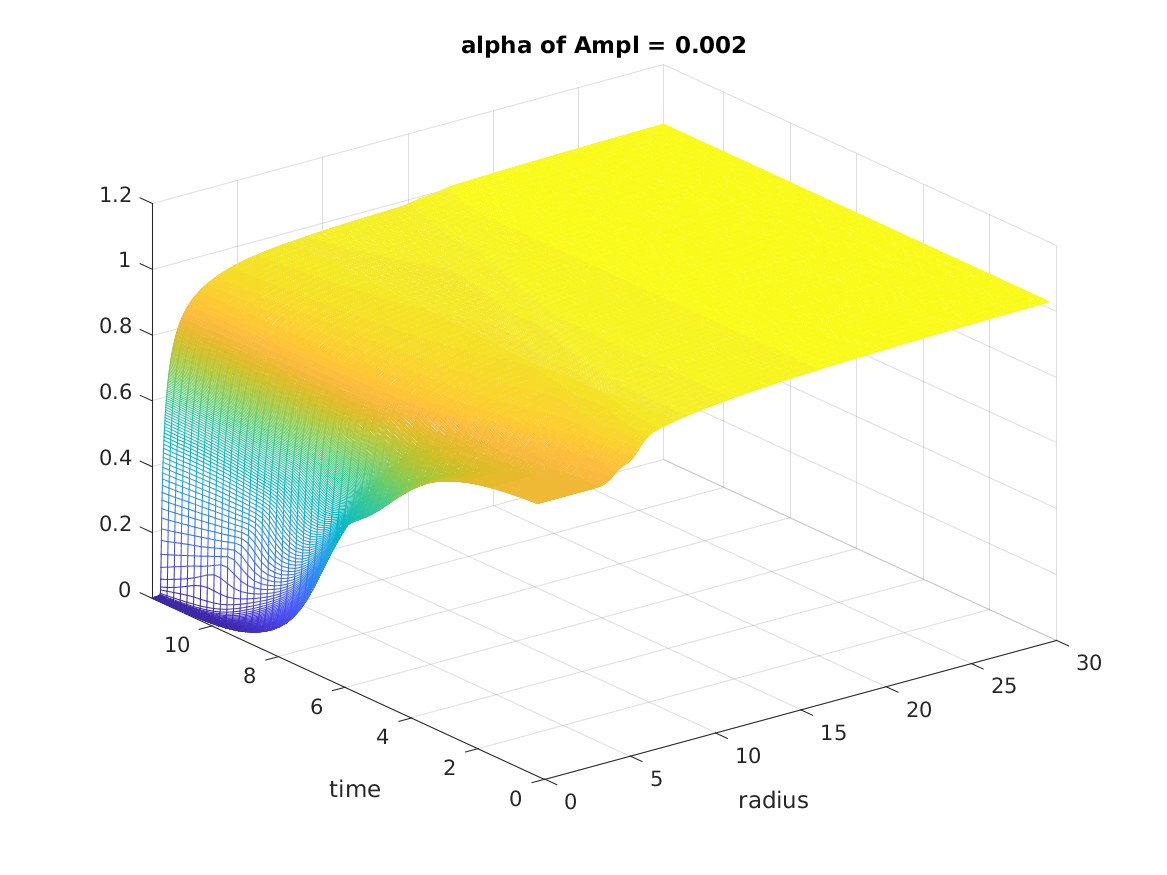
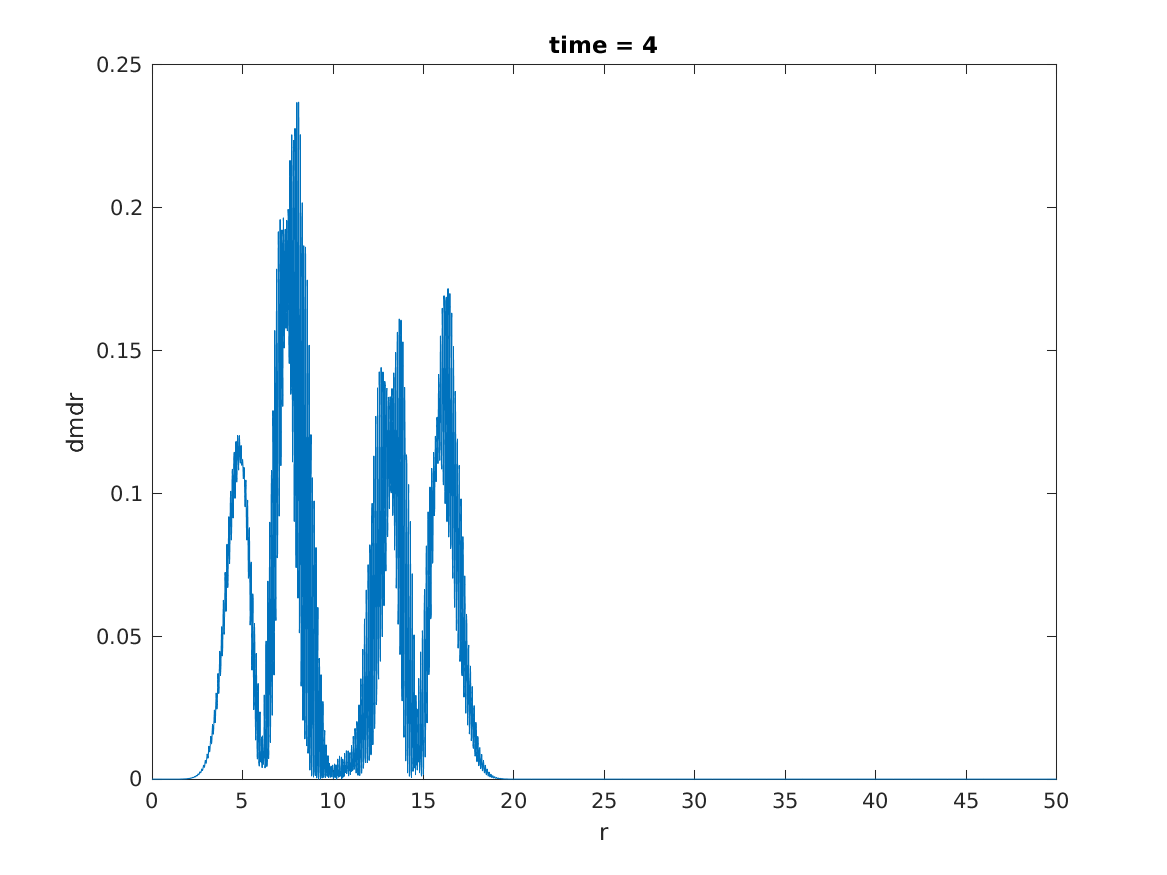
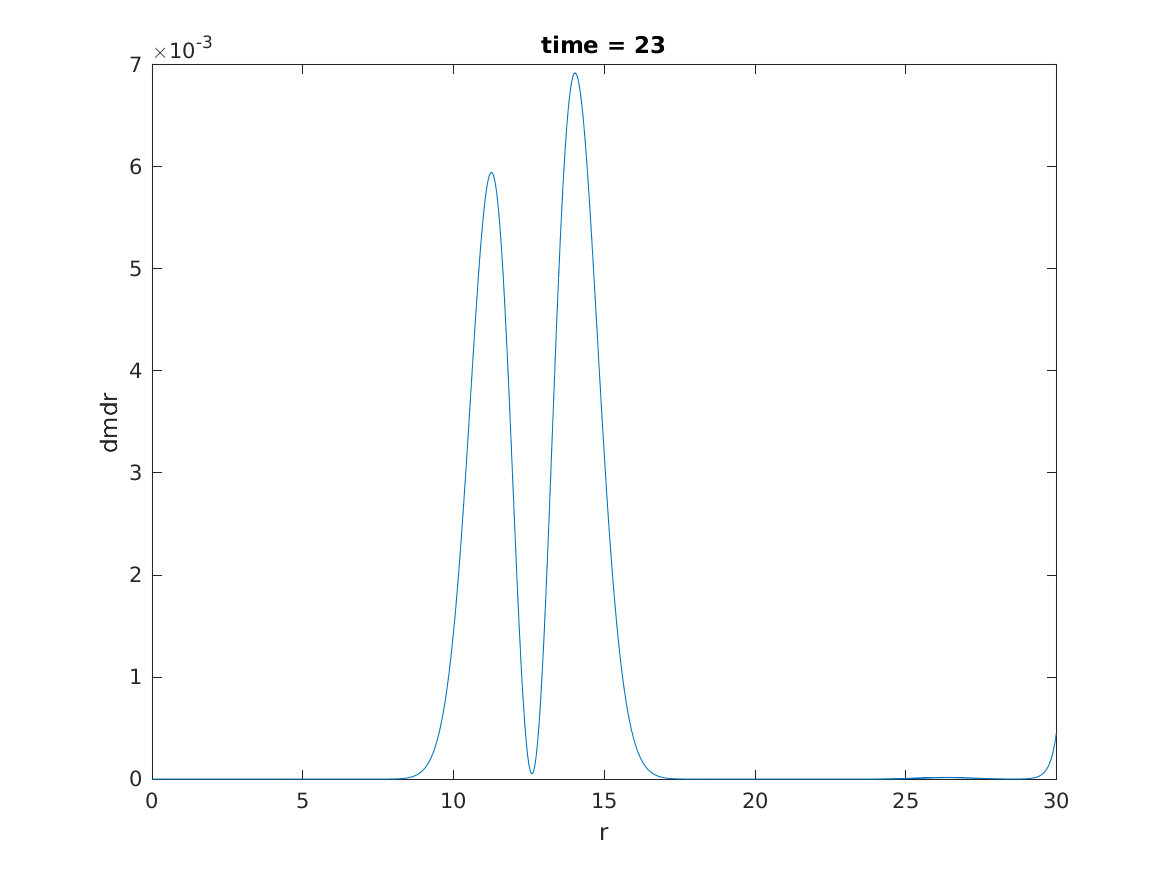
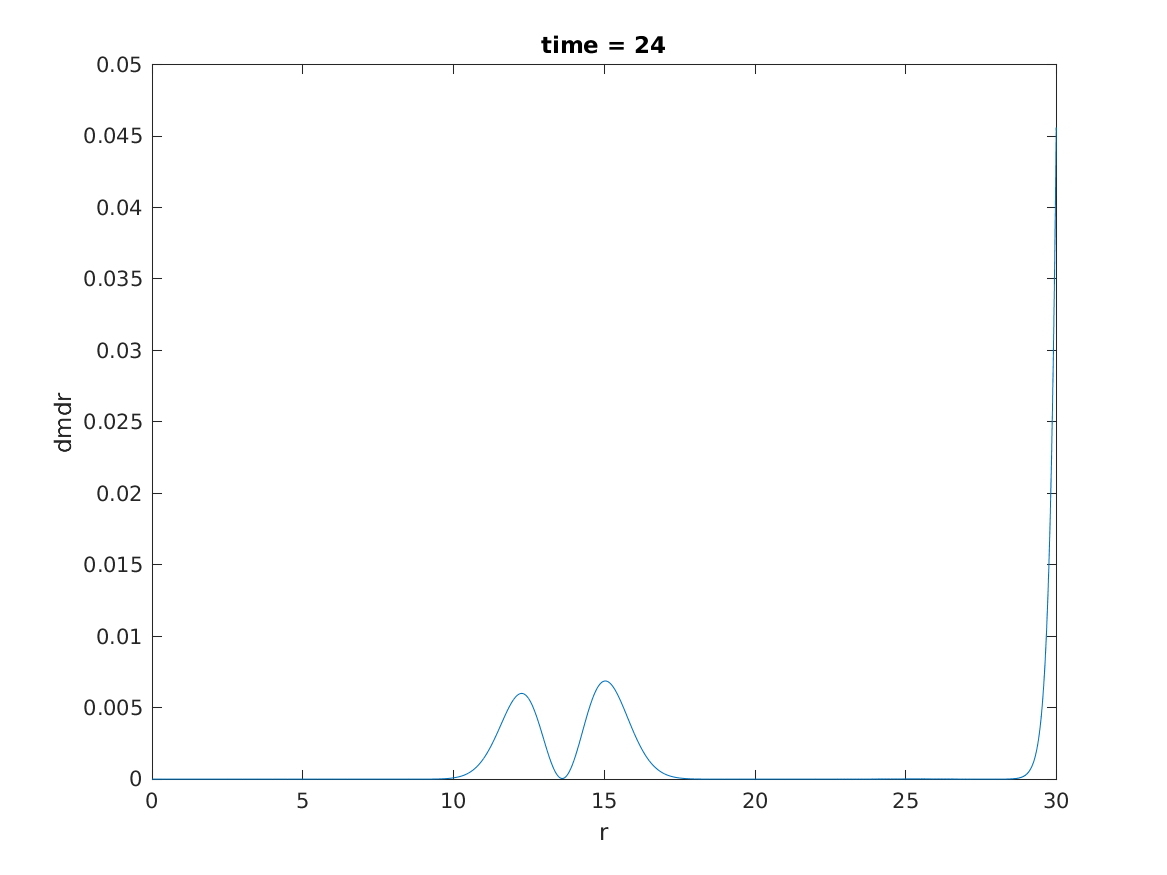
On the other hand, ADM mass \(M_{ADM}\) in computational domain is about 0.54. Then, the mass aspect of black hole is about 0.24 in stable region by the following figure.
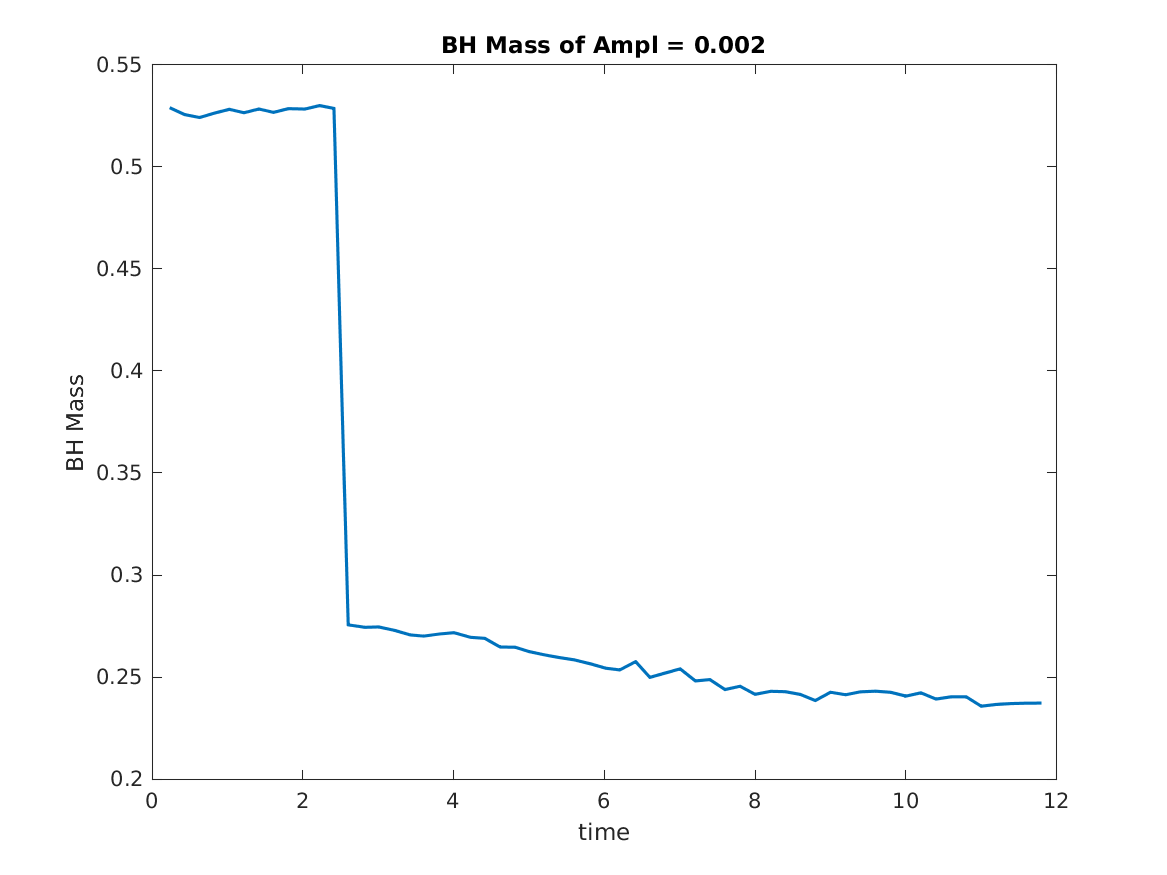
The fact that the mass of final black hole is half the initial ADM mass is to be expected, because the initial pulse divide by two packet: one goes inward and generate black holes and the other escapes to infinity.
Material
Referencess
- R. Arnowitt, S. Deser, C. W. Misner, The Dynamics of General Relativity. Gravitation, (1962).
- M. W. Choptuik, Consistency of finite-difference solutions of Einstein equations, (1991).
- M. W. Choptuik, Universality and Scaling in Gravitational Collapse of a Massless Scalar Field, (1993).
Acknowledgements
I sincerely thank Dr. Peming Ho and Dr. ChunHao Teng for the guidance and assistance.
